
北半球の台風は必ず反時計回り(南半球では必ず時計回り)に回転するが、回転する原因はコリオリ力が働くからである。このコリオリ力が赤道では働かない旨の記事を見かけ違和感を持ったことから、私なりに赤道ではコリオリ力がどうなるのか考えてみた。
違和感を持った経緯
- コリオリ力は、赤道ではゼロである。
- 赤道付近を東西方向に飛ぶ物体は緯度をまたがらないのでコリオリ力は働かない。
- コリオリ力は高緯度ほど大きくなり、赤道では0である。
- コリオリ力f=2Ωsinφ [Ω:角速度、φ:緯度] なので、赤道では緯度φは0となり、コリオリ力fも0となる。
- 赤道上ではコリオリの力の影響は現れない。
- 赤道上には台風は存在しない(コリオリの力が回転に寄与しない)。
私が「赤道ではコリオリ力が働かない」に違和感を持ってしまった理由は、コリオリ力が、ある2つのベクトルのベクトル積(外積)を使った計算式であることをたまたま知っていたからである。ベクトル積が0になるのは2つのベクトルの方向が平行になる時しかなく、つまり、地球上でコリオリ力が働かないことがあるにしても、極限られた場所の極限られたケースにしかない筈なので、感覚的に可笑しいと感じてしまった。
そこで、台風発生のメカニズムについて詳しい訳ではないが、赤道に於いてコリオリ力は具体的にどうなり、それを踏まえて赤道では台風が発生しないと言えるのかを考察してみた。
基礎知識
台風に働くコリオリ力を考える上での基礎知識として、慣性系・非慣性系及び台風が反時計回りになる理由について、以下に述べる。
慣性系・非慣性系
座標系の慣性系と非慣性系の違い、及びこれら座標系の切り分け方について述べる。
慣性系と非慣性系とは
- 慣性系
-
慣性系とは、運動方程式(ニュートンの運動の第2法則)
(力=質量×加速度)
が成り立つ座標系のことである。
砕いて言えば、静止している、あるいは等速直線運動をしている座標系である。例えば、電車に乗らずに地表に立っている観測者から見た世界、あるいは一定速度で直進している電車に乗っている観測者の世界である。
なお、運動方程式が成り立つと言うことは、物体に力を加えなければ加速度は発生しなく、加速度が発生しないと言うことは、静止しているものは静止し続け、動いているものは等速で直線運動し続けることを意味する。つまり、慣性の法則(ニュートンの運動の第1法則)が成り立つので、「慣性系」と言う。 - 非慣性系
-
非慣性系とは、運動方程式が成り立たない座標系のことである。砕いて言えば、等速直線でない運動(加速有りの運動※1)をしている座標系である。例えば、直進していても速くなったり遅くなったりしている電車に乗っている観測者から見た世界、あるいは一定速度であってもカーブを走っている電車に乗っている観測者の世界である。
なお、後述の「コリオリ力(と遠心力)の計算式」でもう少し具体的に説明するが、非慣性系であっても、ニュートンの運動方程式のF(力)に「見かけの力(慣性力)」※2を組み込めば、「質量×加速度=力」の運動方程式が成り立つ。
慣性系は存在するの?
上記の例では、電車に乗らずに地表に立っている観測者の世界は、慣性系と述べた。でも、地表は慣性系なのと疑問を持つ方がいると思う。なぜなら、地球は自転しているので、静止をしていないし等速直線運動もしていないからである。では、地球の自転の影響を受けない地球の外から地球を眺めている観測者の世界は、地球が移動せずに自転しているように見えるので、観測者は慣性系にいるように思える。でも、地球は太陽の周りを公転しており、この観測者も地球の公転に合わせて移動しているので、非慣性系にいることになる。同様に太陽系の外から太陽系を眺めても、太陽系自体が天の川銀河の中心を周回しているので非慣性系にいることになる。更に、銀河群・銀河団、超銀河団※3も重力等の影響を受けて加速度運動していると言ってよいのだろうから、非慣性系である。
そうすると、慣性系はどこにも存在しないことになるが、上記で電車に乗らずに地表に立っている観測者の世界を慣性系と述べた理由は、次のとおりである。
厳密に言えば、地球は自転による加速度運動をしているので、つまり角速度(単位時間に変化する角度のことで、単位は「rad/s」)の影響を受け、見かけの力が発生し慣性系ではない。ただ、地球はゆっくり自転(24時間掛けて1周)しているので、角速度が非常に小さいことから見かけの力も非常に小さくなる。また、公転等では更に角速度が小さくなり、見かけの力も更に小さくなる。
従って、電車のような日常のスケールで体験するような運動を分析する場合は、自転、公転等の加速度運動による見かけの力は無視できる程相対的に小さくなることから、電車に乗っていない観測者の世界を近似的に慣性系と見なすことができる。
その一方で、台風のようにスケールが大きな運動や長時間継続する運動を分析する場合は、自転による見かけの力の影響を無視できなくなり、地球上の観測者の世界は非慣性系となるが、自転の影響を受けない地球の外から地球を眺めている観測者の世界は近似的に慣性系と見なすことができる。
-
銀河群
 数十から100個位の銀河が集まった集団。我々の天の川銀河とアンドロメダ銀河は、同一の銀河群であり、局所銀河群と言う。
数十から100個位の銀河が集まった集団。我々の天の川銀河とアンドロメダ銀河は、同一の銀河群であり、局所銀河群と言う。
-
銀河団
 1000~1万個位の銀河が集まった集団。
1000~1万個位の銀河が集まった集団。
-
超銀河団
 銀河群や銀河団が集まった集団。フィラメント(次の「宇宙の大規模構造」参照)の節目に見つかっているようだ。
銀河群や銀河団が集まった集団。フィラメント(次の「宇宙の大規模構造」参照)の節目に見つかっているようだ。
-
宇宙の大規模構造
 銀河の分布には特徴的な疎密が見られ、大部分の銀河は、銀河団等をつなぐフィラメント状構造に存在しており、このフィラメントに囲まれるようにしてボイド(void:超空洞)と呼ばれる低密度の領域(銀河が殆ど存在しない領域)が存在する。このフィラメント及びボイドが織りなす構造のことを宇宙の大規模構造と言うが、石鹸の泡がくっ付き合っている様子に見えることから泡構造とも言う。
銀河の分布には特徴的な疎密が見られ、大部分の銀河は、銀河団等をつなぐフィラメント状構造に存在しており、このフィラメントに囲まれるようにしてボイド(void:超空洞)と呼ばれる低密度の領域(銀河が殆ど存在しない領域)が存在する。このフィラメント及びボイドが織りなす構造のことを宇宙の大規模構造と言うが、石鹸の泡がくっ付き合っている様子に見えることから泡構造とも言う。
ボイドの直径は約1億~3億光年と言われており、天の川銀河の直径は約10万光年なので、直径で比べるとボイドは天の川銀河の1000~3000倍となる。
宇宙の加速膨張の影響を受け、宇宙の大規模構造は拡大している。その一方で、なぜ天の川銀河とアンドロメダ銀河は離れていかないで接近しているのかと言うと、両銀河間の距離が近過ぎるため、空間の膨張より両銀河間で働く重力の方が強いからである。
遥か将来(1000億年のようなスパン)は、各銀河団や銀河群内の銀河は重力で引き合い、衝突・合体し、1つの巨大銀河になると考えられている。その一方で、1つになった巨大銀河どうしは、両者間で働く重力より空間の加速膨張の方が強いので加速しながら遠ざかって行き、1000億年後の遠ざかる速度は超光速(自然界の最高速度を超える速度)となり、他の全ての巨大銀河から発する光が届かなく観測できなくなると考えられている。
なお、この超光速は、あくまで空間の膨張によるものであり、銀河の運動速度でないので、物体の運動速度は光速を超えられないとする相対性理論に反しておらず。
台風が反時計回りに回転する理由
隣り合う空気の気圧※4に差が発生すると、押し合う力のバランスが崩れ、気圧の高い方(押す力の強い方)から気圧の低い方(押す力の弱い方)へ空気が移動し、風となる。
台風は低気圧の一種であるが、低気圧とは周囲に比べ気圧の低いところを指すので、低気圧の中心に向かって風が吹く。つまり、低気圧の北側にある空気は南側に移動し、南側にある空気は北側に移動し、東側にある空気は西側に移動し、西側にある空気は東側に移動する。
台風を含め低気圧の規模になると、発生する風は中心に向かって直進できなく、北半球であれば反時計回りに中心へと集まる(南半球では時計回り)。その理由は上記でも少し触れたが、地球と一緒に自転している大気は、常に加速(地球と同様に回転)しているので非慣性系であり、風(大気中を運動している空気)には自転による見かけの力(コリオリ力)を受けるからである。この時に発生するコリオリ力は北半球では空気の流れの進行方向に対し右向きの力(図1の緑色矢印)となる(南半球では左向きの力になる)。なお、コリオリ力の発生と向きの詳細説明については、後述の「赤道ではコリオリ力が働かないの?」を参照されたし。
そうすると、北半球では直進する筈の空気(図1の灰色矢印)が右へ右へと向きが変わってしまい(図1の水色矢印)、これにより台風は反時計回りに回転する(図1の紺色矢印)。南半球では逆に、直進する筈の空気が左へ左へと向きが変わってしまい、これにより台風は時計回りに回転する。

ある場所の空気はそれより上のに存在する空気の重さがのし掛かっているので上から押され、下へ移動しようとするも下には地面や空気があるため押し返され、横に移動しようとするも、そこには別の空気があるため押し返され、四方八方で押し合いバランスが取れている。気圧とは、この単位面積当たりの押し合う力であり、ある場所より上にある空気の重さによる圧力と言うこともできる。
赤道ではコリオリ力が働かないの?
ここから本題に入って行く。
コリオリ力がどの方向にどれだけの力が働くかを知るには、コリオリ力の計算式を知らないと話にならないので、まずはコリオリ力の計算式を示し、その計算式を元に赤道のコリオリ力について考察する。
なお、コリオリ力の計算式は自転している地球上の運動方程式を導き出すことにより求まるが、導出に興味のある方は「自転に於ける運動方程式の導出」を参照されたし。
コリオリ力(と遠心力)の計算式
-
細字
 スカラー
スカラー
-
太字
 ベクトル
ベクトル
-
文字にダッシュ有り
 非慣性系(地球上)から見た物理量
非慣性系(地球上)から見た物理量
-
\( m \)
 物体の質量
物体の質量
-
\( \boldsymbol{ v } \)
 物体の速度ベクトル
物体の速度ベクトル
-
\( \boldsymbol{ a } \)
 物体の加速度ベクトル
物体の加速度ベクトル
-
\( ω \)
 角速度。回転運動している平面に於いて、動径(回転する半直線のこと)が単位時間当たりに回転する角度のこと。
角速度。回転運動している平面に於いて、動径(回転する半直線のこと)が単位時間当たりに回転する角度のこと。
-
\( \boldsymbol{ ω } \)
 角速度ベクトル。角速度ωの絶対値を大きさとし、 回転軸方向(回転面が反時計回りに見える方向)を向いたベクトルである。
角速度ベクトル。角速度ωの絶対値を大きさとし、 回転軸方向(回転面が反時計回りに見える方向)を向いたベクトルである。
-
\( \boldsymbol{ r } \)
 地軸から垂直に物体へ向かう位置ベクトル
地軸から垂直に物体へ向かう位置ベクトル
-
\( \boldsymbol{ F } \)
 ニュートンの運動の第2法則上の力ベクトル
ニュートンの運動の第2法則上の力ベクトル
-
\( \times \)
 ベクトル積(外積)の演算子
ベクトル積(外積)の演算子
-
+
 四則演算の足し算の演算子
四則演算の足し算の演算子
導出過程に於いて微分やベクトルを使用しており、主にベクトルの知識がない方を意識して解説している。そこで導出に入る前に、基礎知識としてベクトルの性質や微分の記法について、以下に纏めておく。
- ベクトル積の性質
-
ベクトル積(外積)の演算子は「×」であり(例えば、\( \boldsymbol{ a } \)と \( \boldsymbol{ b } \)のベクトル積は「 \( \boldsymbol{ a } \times \boldsymbol{ b } \)」)、外積の計算結果がベクトルになるので「ベクトル積」と言う。
ベクトル積の性質は次のとおりであるが、成り立たないものがあるので注意されたし。- スカラー倍
-
\(
\boldsymbol{ a } \times ( k \boldsymbol{ b } )
= ( k \boldsymbol{ a } ) \times \boldsymbol{ b }
= k ( \boldsymbol{ a } \times \boldsymbol{ b } )
\)
\(
( k \boldsymbol{ a } ) \times ( l \boldsymbol{ b } )
= ( k l ) ( \boldsymbol{ a } \times \boldsymbol{ b } )
\) - 交換法則
-
\(
\boldsymbol{ a } \times \boldsymbol{ b }
= – \boldsymbol{ b } \times \boldsymbol{ a }
\)※ベクトルの大きさは同じだが、向きが逆になるため成り立たず! - 分配法則
-
\(
( \boldsymbol{ a } + \boldsymbol{ b } ) \times \boldsymbol{ c }
= \boldsymbol{ a } \times \boldsymbol{ c } + \boldsymbol{ b } \times \boldsymbol{ c }
\)
\(
\boldsymbol{ a } \times ( \boldsymbol{ b } + \boldsymbol{ c } )
= \boldsymbol{ a } \times \boldsymbol{ b } + \boldsymbol{ a } \times \boldsymbol{ c }
\) - 結合法則
-
\(
( \boldsymbol{ a } \times \boldsymbol{ b } ) \times \boldsymbol{ c }
\neq \boldsymbol{ a } \times ( \boldsymbol{ b } \times \boldsymbol{ c } )
\)※成り立たず! - 三重積
-
\(
\boldsymbol{ a } \times ( \boldsymbol{ b } \times \boldsymbol{ c } )
= ( \boldsymbol{ a } \cdot \boldsymbol{ c } ) \boldsymbol{ b } – ( \boldsymbol{ a } \cdot \boldsymbol{ b } ) \boldsymbol{ c }
= \boldsymbol{ b } ( \boldsymbol{ a } \cdot \boldsymbol{ c } ) – \boldsymbol{ c } ( \boldsymbol{ a } \cdot \boldsymbol{ b } )
\)※ベクトル積の計算結果はベクトル(また、ベクトルのスカラー倍もベクトル)なので、上式の計算結果もベクトル
- スカラー積の性質
-
スカラー積(内積)の演算子は「・」であり(例えば、\( \boldsymbol{ a } \)と \( \boldsymbol{ b } \)のスカラー積は「 \( \boldsymbol{ a } \cdot \boldsymbol{ b } \)」)、内積の計算結果がスカラーになるので「スカラー積」と言う。スカラー積の性質は次のとおりである。
- スカラー倍
-
\(
\boldsymbol{ a } \cdot ( k \boldsymbol{ b } )
= ( k \boldsymbol{ a } ) \cdot \boldsymbol{ b }
= k ( \boldsymbol{ a } \cdot \boldsymbol{ b } )
\)
\(
( k \boldsymbol{ a } ) \cdot ( l \boldsymbol{ b } )
= ( k l ) ( \boldsymbol{ a } \cdot \boldsymbol{ b } )
\) - 交換法則
-
\(
\boldsymbol{ a } \cdot \boldsymbol{ b }
= \boldsymbol{ b } \cdot \boldsymbol{ a }
\) - 分配法則
-
\(
( \boldsymbol{ a } + \boldsymbol{ b } ) \cdot \boldsymbol{ c }
= \boldsymbol{ a } \cdot \boldsymbol{ c } + \boldsymbol{ b } \cdot \boldsymbol{ c }
\)
\(
\boldsymbol{ a } \cdot ( \boldsymbol{ b } + \boldsymbol{ c } )
= \boldsymbol{ a } \cdot \boldsymbol{ b } + \boldsymbol{ a } \cdot \boldsymbol{ c }
\) - 結合法則
-
\(
( \boldsymbol{ a } \cdot \boldsymbol{ b } ) \cdot \boldsymbol{ c }
= \boldsymbol{ a } \cdot ( \boldsymbol{ b } \cdot \boldsymbol{ c } )
\) - 三重積
-
\(
\boldsymbol{ a } \cdot ( \boldsymbol{ b } \times \boldsymbol{ c } )
= \boldsymbol{ b } \cdot ( \boldsymbol{ c } \times \boldsymbol{ a } )
= \boldsymbol{ c } \cdot ( \boldsymbol{ a } \times \boldsymbol{ b } )
\)※スカラー積の計算結果はスカラーなので、上式の計算結果もスカラー - その他
-
\(
\boldsymbol{ a } \cdot \boldsymbol{ a }
= | \boldsymbol{ a } | ^ 2
= a ^ 2
\)※\( \boldsymbol{ a } \)の大きさの2乗
-
\( \boldsymbol{ A } \) 、\( \boldsymbol{ B } \)
 スカラー変数t(時間)のベクトル関数\( \boldsymbol{ A } (t) \) 、\( \boldsymbol{ B } (t) \)のことで、引数\( (t) \)を省略した表現
スカラー変数t(時間)のベクトル関数\( \boldsymbol{ A } (t) \) 、\( \boldsymbol{ B } (t) \)のことで、引数\( (t) \)を省略した表現
-
\( f \)
 スカラー変数t(時間)のスカラー関数\( { f } (t) \)のことで、引数\( (t) \)を省略した表現
スカラー変数t(時間)のスカラー関数\( { f } (t) \)のことで、引数\( (t) \)を省略した表現
-
\( α \)
 スカラー定数
スカラー定数
- スカラー定数倍の微分
-
※スカラー関数の様にスカラー定数を微分の外に出せる。
- スカラー関数倍の微分
-
※スカラー関数の積の微分の公式の様な式が成り立つ。
- 和・差の微分
-
※スカラー関数の様に、各関数の微分に対する和・差が成り立つ。
- スカラー積の微分
-
※スカラー関数の積の微分の公式の様な式が成り立つ。
- ベクトル積の微分
-
※スカラー関数の積の微分の公式の様な式が成り立つが、ベクトル積の順序を入れ替えると符号が変わるので注意!(例えば、\( \require{physics} \dv{ \boldsymbol{ A } } { t } \times \boldsymbol{ B } = – \boldsymbol{ B } \times \require{physics} \dv{ \boldsymbol{ A } } { t } \) )
| 微分の階数 | ライプニッツの記法 [読み方] |
ニュートンの記法 [読み方] |
|---|---|---|
| 一階微分 |
\( \require{physics} \dv{ y }{ t } \) [ディー ワイ ディー ティー] |
\( \dot{y} \) [ワイ ドット] |
| 二階微分 |
\( \require{physics} \dv[2]{ y }{ t } \) [ディー ツー ワイ ディー ティー ツー] |
\( \ddot{y} \) [ワイ ダブル ドット] |
ChatGPTに使われるAIがGPTと言う大規模言語モデル(LLM)である。GPTはTransformer[トランスフォーマー]の技術を元に作られており、Transformerは単語どうしの関係を広く把握し、どの単語とどの単語が意味的に近いのかを学習することができるアルゴリズムである。Transformerでは、各単語をベクトルに変換し、ベクトルどうしの距離の近さ(単語の意味の近さ)の指標を、スカラー積を使って計算している。
ベクトル終点の2点間の距離を求めるのでなく、スカラー積を使うメリットは次のとおり。
- メリット1
-
単語どうしの関連性と各単語の重要度(影響力)の大きさの両方を評価できる。
- 関連性
-
2つの単語の意味が近い程、単語のベクトルの向きは近づくように設定されている。と言うことは、2つの単語のベクトルが成す角をθとするとcosθは、0≦θ≦180°の範囲で、ベクトルの成す角θが小さいほど値が大きくなり、つまり\( \cos θ \)の値が大きいほど、2つの単語の関連性が強いことを示すことになる。
この\( \cos θ \)の値は、スカラー積の定義 \( \boldsymbol { a } \cdot \boldsymbol { b } = | \boldsymbol { a } | | \boldsymbol { b } | \cos θ \)から分かるように、\( \cos θ = \frac{ \boldsymbol { a } \cdot \boldsymbol { b } }{ | \boldsymbol { a } | | \boldsymbol { b } | } \)である(なお、この式は高次元に於けるベクトルの成す角の定義を意味する)。よって、\( \boldsymbol { a } \cdot \boldsymbol { b } \)(スカラー積)、及び\( | \boldsymbol { a } | \)と\( | \boldsymbol { b } | \)(各ベクトルの大きさ)を求められれば、\( \cos θ \)の値を求めることができる。
\( \boldsymbol { a } \cdot \boldsymbol { b } \)(スカラー積)に関しては、各ベクトルを成分表示したスカラー積の定義、つまり同じ成分同士を掛けたものを、足し合わせれば求まる。
\( | \boldsymbol { a } | \)と\( | \boldsymbol { b } | \)(各ベクトルの大きさ)に関しては、例えば\( \boldsymbol { a } \)の大きさは\( | \boldsymbol { a } | = \sqrt{ \boldsymbol { a } \cdot \boldsymbol { a } } \)なので、\( \boldsymbol { a } \cdot \boldsymbol { a } \)を成分表示したスカラー積の定義で計算し、その値に対し平方根を取れば求まる。 - 影響力
- 文章全体の意味に与える影響力の大きい単語は、ベクトルの大きさが大きく設定されている。なので、影響力の大きい単語ベクトルどうしのスカラー積ほど、その値が大きくなる。
- メリット2
-
成分表示したスカラー積の計算は簡単である。
空間上の2点間の距離を計算するには、(ピタゴラスの定理から分かるように)同じ成分同士の差を2乗したものを、足し合わせた後に平方根を取る必要があり、計算が複雑である。一方、2つのベクトルのスカラー積は、成分表示したスカラー積の定義を使って求めればよく、計算が簡単である。
なお、基礎技術であるTransformerは、文章生成のみならず幅広い分野に応用されている。
ここから導出の本題に入る。
\( S \)系は慣性系であり、\( S’ \)系は非慣性系で、\( S \)系に対し並進運動せずに単に反時計回りの回転運動のみをし(回転座標系)、角速度ベクトル\( \boldsymbol {ω} \)で回転しているものとする。また、\( S \)系と\( S’ \)系は次のことが一致しているものとする(図2参照)。
- \( S \)系の\( z \)軸と\( S’ \)系の\( z’ \)軸は、共に\( S’ \)系の回転軸と一致する(\( \boldsymbol {ω} \)の向きはz’軸の正の方向と一致)。
- \( S \)系の原点\( O \)と\( S’ \)系の原点\( O’ \)は一致し、回転軸上にある。
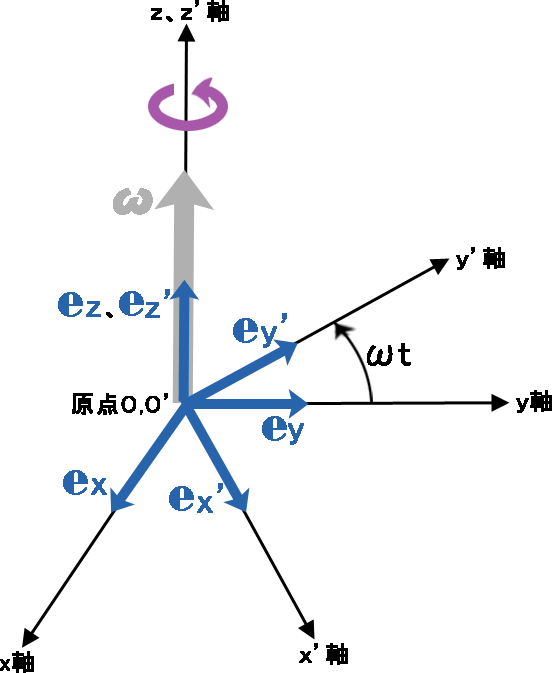
「\( \boldsymbol{ e } \)」は、単位ベクトル(大きさ1のベクトル)を示す。特に、座標系の各軸の正方向を向いた単位ベクトルを「基本ベクトル」と言う。本記事に於いては、例えば「\( \boldsymbol{ e_x } \)」なら\( S \)系の\( x \)軸の基本ベクトル、「\( \boldsymbol { e_{x’} } \)」なら\( S’ \)系の\( x’ \)軸の基本ベクトルを意味する。
-
\( \boldsymbol{ r } \)
 \( S \)系から眺めた質点の位置ベクトル(始点は原点\( O \)であり\( O’ \)でもある)。
\( S \)系から眺めた質点の位置ベクトル(始点は原点\( O \)であり\( O’ \)でもある)。
-
\( \boldsymbol { r }’ \)
 \( S’ \)系から眺めた質点の位置ベクトル(始点は原点\( O’ \)であり\( O \)でもある)。
\( S’ \)系から眺めた質点の位置ベクトル(始点は原点\( O’ \)であり\( O \)でもある)。
- 「ベクトル関数の微分の性質」の「和の微分」により、各項に対して微分。
- 各項の微分は、「ベクトル関数の微分の性質」の「スカラー関数倍の微分」を利用。
- \( \boldsymbol { e } \)について
-
\( \boldsymbol { e_x } \) 、 \( \boldsymbol { e_y } \) 、 \( \boldsymbol { e_z } \)は、慣性系の基本ベクトルなので、時間\( t \)の経過に伴い座標軸の向きは変化しない。従って、時間\( t \)で微分すると\( \dot { \boldsymbol { e_x } } = \dot { \boldsymbol { e_y } } = \dot { \boldsymbol { e_z } } = \boldsymbol { 0 } \) ……①となる。
- \( \boldsymbol { e }’ \)について
-
\( \boldsymbol { e_{x’} } \) 、 \( \boldsymbol { e_{y’} } \) 、 \( \boldsymbol { e_{z’} } \)は、非慣性系(回転座標系)なので、時間\( t \)の経過に伴い座標軸の向きが変化する。従って、時間\( t \)で微分しても\( \boldsymbol { 0 } \)にならない。
回転軸に対し\( \boldsymbol { ω } \)で回転している任意のベクトル\( \boldsymbol { A } \)の時間的変化率(回転している\( \boldsymbol { A } \)の向きの変化率)は、 時間的変化率の証明以下に、\( \boldsymbol { A } \)の時間的変化率(\( \dot { \boldsymbol{ A } } \))が、\( \boldsymbol { ω } \)を用いたベクトル積(\( \boldsymbol { \boldsymbol{ ω } \times \boldsymbol{ A } } \))になることを証明する。
時間的変化率の証明以下に、\( \boldsymbol { A } \)の時間的変化率(\( \dot { \boldsymbol{ A } } \))が、\( \boldsymbol { ω } \)を用いたベクトル積(\( \boldsymbol { \boldsymbol{ ω } \times \boldsymbol{ A } } \))になることを証明する。
ベクトルは向きと大きさを与えれば決定するので、回転の様子は\( \boldsymbol { A } \)と\( \boldsymbol { ω } \)の始点を一致させて、図3のように描くことができる。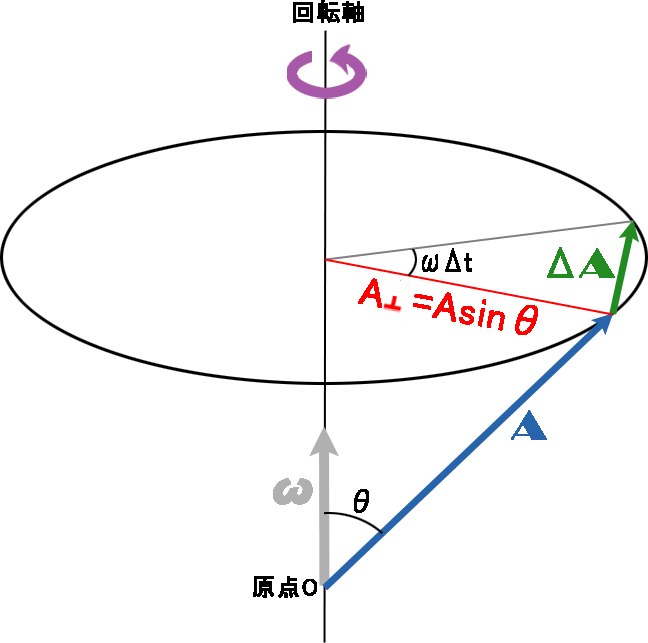 図3 ベクトルの回転この時、\( \Delta \boldsymbol { A } \)の向きと大きさについて次のことが言える。
図3 ベクトルの回転この時、\( \Delta \boldsymbol { A } \)の向きと大きさについて次のことが言える。- 向き
-
時間\( \Delta t \)の間の\( \boldsymbol { A } \)の変化\( \Delta \boldsymbol { A } \)は、図3から明らかであるが、\( \boldsymbol { ω } \)と\( \boldsymbol { A } \)の両方に垂直となる(\( \Delta \boldsymbol { A } \bot \boldsymbol { ω } \)、\( \Delta \boldsymbol { A } \bot \boldsymbol { A } \))。
つまり、\( \Delta \boldsymbol { A } \)は\( \boldsymbol{ ω } \times \boldsymbol{ A } \)の向きと一致している(「ベクトル積の定義」を参照)。 - 大きさ
-
\( \boldsymbol { ω } \)と\( \boldsymbol { A } \)の間の角度を\( θ \)とし、\( \boldsymbol { A } \)の\( \boldsymbol { ω } \)に垂直な成分を\( A_{ \bot } \)とすると、\( \Delta \boldsymbol { A } \)の大きさは、\begin{align}
|\Delta \boldsymbol { A }| &\approx A_{ \bot } |\boldsymbol { ω }| \Delta t \\
&= ωA \sin θ \Delta t
\end{align}※ 補足-
\( A_{ \bot } |\boldsymbol { ω }| \)
 1秒間の回転で移動した弧の長さ
1秒間の回転で移動した弧の長さ
- \( A_{ \bot } = |\boldsymbol { A }| \sin θ = A \sin θ \)
となる。
つまり、\( ωA \sin θ \)は\( \boldsymbol { \boldsymbol{ ω } \times \boldsymbol{ A } } \)の大きさであり(「ベクトル積の定義」を参照)、よって\( \Delta \boldsymbol { A } \)の大きさは、\( \boldsymbol { \boldsymbol{ ω } \times \boldsymbol{ A } } \)の大きさに\( \Delta t \)を掛けた値にほぼ等しい。 -
\( A_{ \bot } |\boldsymbol { ω }| \)
以上から、ベクトル積を用いれば、大きさだけでなく向きを含めて、\begin{align}
\Delta \boldsymbol { A } \approx \boldsymbol { \boldsymbol{ ω } \times \boldsymbol{ A } } \Delta t
\end{align}と表すことができ、両辺を\( \Delta t \)で割って、\( \Delta t \to 0 \)の極限をとると、となる。なので、次のことが成り立つ。\( \dot { \boldsymbol { e_{x’} } } = \boldsymbol{ ω } \times \boldsymbol { e_{x’} } \) 、 \( \dot { \boldsymbol { e_{y’} } } = \boldsymbol{ ω } \times \boldsymbol { e_{y’} } \) 、 \( \dot { \boldsymbol { e_{z’} } } = \boldsymbol{ ω } \times \boldsymbol { e_{z’} } \) ……②
ちなみに、④は両座標系での位置ベクトルの関係式(②)を時間微分しているので、両座標系での速度ベクトルの関係式として、次のように表すことができる。
- \( S \)系による質点運動
-
\( S \)系の座標が基準なので、この座標系そのものの運動は見えない。従って、座標系が運動しているか否かに関係なく、質点の運動は、質点の位置ベクトルがであれば、次のとおりになる。なお、この基準では、\( \dot { \boldsymbol { e_x } } = \dot { \boldsymbol { e_y } } = \dot { \boldsymbol { e_z } } = \boldsymbol { 0 } \)となるので、「スカラー関数倍の微分」を行った時に、\( \dot { \boldsymbol { e } } \)が付く項は全て\( \boldsymbol { 0 } \)となる。
-
質点の速度ベクトル
 \( \dot { \boldsymbol { r } } = \boldsymbol { v } = \dot { x } \boldsymbol { e_x } + \dot { y } \boldsymbol { e_y } + \dot { z } \boldsymbol { e_z } \) ……④
\( \dot { \boldsymbol { r } } = \boldsymbol { v } = \dot { x } \boldsymbol { e_x } + \dot { y } \boldsymbol { e_y } + \dot { z } \boldsymbol { e_z } \) ……④
-
質点の加速度ベクトル
 \( \ddot { \boldsymbol { r } } = \boldsymbol { a } = \ddot { x } \boldsymbol { e_x } + \ddot { y } \boldsymbol { e_y } + \ddot { z } \boldsymbol { e_z } \) ……⑤
\( \ddot { \boldsymbol { r } } = \boldsymbol { a } = \ddot { x } \boldsymbol { e_x } + \ddot { y } \boldsymbol { e_y } + \ddot { z } \boldsymbol { e_z } \) ……⑤
-
質点の速度ベクトル
- \( S’ \)系による質点運動
-
\( S’ \)系の座標が基準なので、この座標系そのものの運動は見えない。従って、座標系が運動しているか否かに関係なく、質点の運動は、質点の位置ベクトルがであれば、次のとおりになる。なお、この基準では、\( \dot { \boldsymbol { e_{x’} } } = \dot { \boldsymbol { e_{y’} } } = \dot { \boldsymbol { e_{z’} } } = \boldsymbol { 0 } \)となるので、「スカラー関数倍の微分」を行った時に、\( \dot { \boldsymbol { e }’ } \)が付く項は全て\( \boldsymbol { 0 } \)となる。
-
質点の速度ベクトル
 \( \dot { \boldsymbol { r }’ } = \boldsymbol { v }’ = \dot { x’ } \boldsymbol { e_{x’} } + \dot { y }’ \boldsymbol { e_{y’} } + \dot { z’ } \boldsymbol { e_{z’} } \) ……⑦
\( \dot { \boldsymbol { r }’ } = \boldsymbol { v }’ = \dot { x’ } \boldsymbol { e_{x’} } + \dot { y }’ \boldsymbol { e_{y’} } + \dot { z’ } \boldsymbol { e_{z’} } \) ……⑦
-
質点の加速度ベクトル
 \( \ddot { \boldsymbol { r }’ } = \boldsymbol { a’ } = \ddot { x’ } \boldsymbol { e_{x’} } + \ddot { y’ } \boldsymbol { e_{y’} } + \ddot { z’ } \boldsymbol { e_{z’} } \) ……⑧
\( \ddot { \boldsymbol { r }’ } = \boldsymbol { a’ } = \ddot { x’ } \boldsymbol { e_{x’} } + \ddot { y’ } \boldsymbol { e_{y’} } + \ddot { z’ } \boldsymbol { e_{z’} } \) ……⑧
-
質点の速度ベクトル
- 左辺の微分
-
「\(
\dot{x} \boldsymbol { e_x }
+ \dot{y} \boldsymbol { e_y }
+ \dot{z} \boldsymbol { e_z }
\)」を微分すると、1階微分の解説と同様に(②の左辺の微分を参照)、各項に対し「スカラー関数倍の微分」を行った上で、①を代入する。となる。 - 右辺の「\( \boldsymbol { ω } \)」が付かない3項の微分
-
「\(
\dot{x’} \boldsymbol { e_{x’} }
+ \dot{y’} \boldsymbol { e_{y’} }
+ \dot{z’} \boldsymbol { e_{z’} }
\)」を微分すると、1階微分の解説と同様に(②の右辺の微分を参照)、次のことを行う。- 各項に対し「スカラー関数倍の微分」を行った上で、②を代入することにより\( \dot{ \boldsymbol { e }’ } \)を使用しない式にする。
- 「ベクトル積の性質」を利用して整理する(括弧で括り\( \boldsymbol { ω } \)を括弧の外に出す)。
となる。 - 右辺の「\( \boldsymbol { ω } \)」が付く項の微分
-
「\(
\boldsymbol { ω } \times ( x’ \boldsymbol { e_{x’} } + y’ \boldsymbol { e_{y’} } + z’ \boldsymbol { e_{z’} } )
\)」を微分する。「ベクトル関数の微分の性質」の「ベクトル積の微分」を利用。地球は等速円運動をしているので、角速度ベクトル\( \boldsymbol { ω } \)は時間の経過に伴い変化することはなく一定である。従って、「\( \dot { \boldsymbol { ω } } = \boldsymbol { 0 } \)」であり、1項目が消える。「ベクトル関数の微分の性質」の「スカラー関数倍の微分」を利用。「ベクトル積の性質」の「分配法則」を利用して、2つの括弧で(\( \boldsymbol { e}’ \)グループと\( \dot{ \boldsymbol { e}’ } \)グループに)分ける。2項目の括弧内(\( \dot{ \boldsymbol { e}’ } \)グループ)に対して、次のことを行う。- ②を代入することにより\( \dot{ \boldsymbol { e }’ } \)を使用しない式にする。
- 「ベクトル積の性質」を利用して整理する(括弧で括り\( \boldsymbol { ω } \)を括弧の外に出す)。
以上により、④の両辺に対して時間微分すると、「⑥=⑦+⑧」であり、となり、更に整理すると同じベクトルの足し算は、向きは変わらないが大きさが2倍になるので(\( \boldsymbol { a } + \boldsymbol { a } = 2 \boldsymbol { a } \))、同じベクトルの項を1つの項に纏める。となり、⑤~⑧を代入すると、となり、両座標系で加速度の関係式となる。次に、ニュートンの運動方程式「\( m \boldsymbol { a } = \boldsymbol { F } \)」に⑨を代入するととなり、左辺を展開するととなり、\( S’ \)系から眺めた運動方程式は、となる。
⑩は、ニュートンの運動方程式と異なり、右辺の2項目と3項目が追加されていることからも、\( S’ \)系は慣性系でないことが分かる。この2項目と3項目が慣性力(見かけの力)であり、2項目を「コリオリ力」、3項目を「遠心力」と呼ぶ。最後に、求まった慣性力の式を扱い易い式に変える。- コリオリ力
-
「\( – \ 2m \boldsymbol { ω } \times \boldsymbol { v }’ \)」だと、マイナスが付くのでプラスの式に直す。
「ベクトル積の性質」で述べたとおり、「交換法則」が成り立たなく、ベクトルの順番を入れ替えると向きが逆になる(符号が反転する)。つまり、マイナスからプラスに反転させるには、ベクトルの順番を入れ替えれば良い。
従ってコリオリ力の計算式は、となる。 - 遠心力
-
「ベクトル積の性質」の「三重積」を利用して、ベクトル積を無くしスカラー積の計算式にする。
-
1項目
 「スカラー積の性質」の「その他」( \( \boldsymbol{ a } \cdot \boldsymbol{ a } = a ^ 2 \))を利用。
「スカラー積の性質」の「その他」( \( \boldsymbol{ a } \cdot \boldsymbol{ a } = a ^ 2 \))を利用。
-
2項目
 「スカラー積の性質」の「交換法則」を利用。
「スカラー積の性質」の「交換法則」を利用。
\( \boldsymbol { ω } \)方向の単位ベクトルを\( \boldsymbol { e_ω } \)とすると、\( \boldsymbol { ω } = ω \boldsymbol { e_ω } \)となり、これを代入する。「スカラー積の性質」の「スカラー倍」を利用。\( \boldsymbol { r }’ \cdot \boldsymbol { e_ω } ={r_ω}’ \)を代入する。※ 補足
\( \boldsymbol { r }’ \)と\( \boldsymbol { e_ω } \)(\( \boldsymbol { ω } \)方向の単位ベクトル)の成す角度を\( \boldsymbol { θ } \)とすると、スカラー積の定義により\( \boldsymbol { r }’ \cdot \boldsymbol { e_ω } = | \boldsymbol { r }’ | | \boldsymbol { e_ω } | \cos θ \)となり、\( | \boldsymbol { e_ω } | = 1 \)なので\( | \boldsymbol { r }’ | \cos θ = r’ \cos θ \)となる。
つまりり\( \boldsymbol { r }’ \cdot \boldsymbol { e_ω } \)は、\( \boldsymbol { r }’ \)に対する\( \boldsymbol { ω } \)軸成分の大きさを意味する。この大きさを\( {r_ω}’ \)と置くと、\( \boldsymbol { r }’ \cdot \boldsymbol { e_ω } = {r_ω}’ \)となる。そうすると、図4の紺色ベクトルは\( {r_ω}’ \boldsymbol { e_ω } \)となり、緑色ベクトルは\( r’ – {r_ω}’ \boldsymbol { e_ω } \)となる。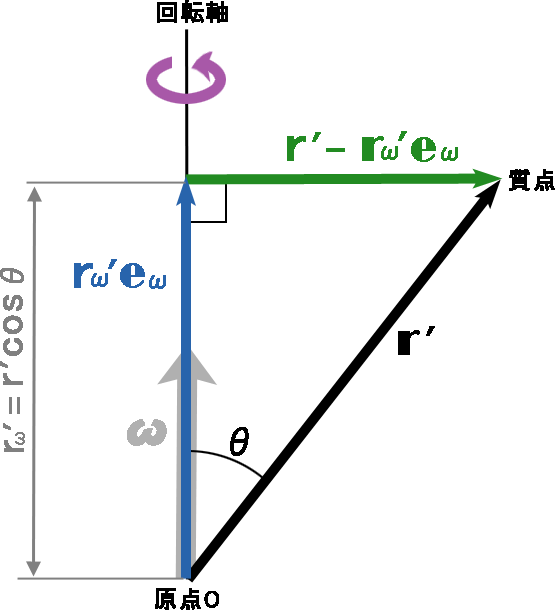 図4 回転軸から質点に向かうベクトル\( \boldsymbol { r }’ – {r_ω}’ \boldsymbol { e_ω } = \boldsymbol { \xi }’ \)とし、代入する。※ 補足
図4 回転軸から質点に向かうベクトル\( \boldsymbol { r }’ – {r_ω}’ \boldsymbol { e_ω } = \boldsymbol { \xi }’ \)とし、代入する。※ 補足
\( \boldsymbol { \xi }’ \)(図4の緑色ベクトル)を地球に当てはめると、地上にある質点と垂直にある地軸の位置を原点に取り、原点から質点に向かうベクトルを意味する。
なお、\( \boldsymbol { \xi } \)の読み方は、「グザイ」(「クサイ」、「クシー」)である。となり、従って遠心力の計算式は、となる。以上を纏めると、自転している地球上(非慣性系の\( S’ \)系)の運動方程式は、⑩に⑪と⑫を代入することにより、次のとおりとなる。※ 注意(\( \boldsymbol { r }’ \)について)
本導出の解説では、回転軸上にある原点\( O’ \)を始点とした質点の位置ベクトルを\( \boldsymbol { r }’ \)と定義したので、地軸から垂直に質点に向かうベクトルは\( \boldsymbol { r }’ \)を使用せず\( \boldsymbol { \xi }’ \)を使用した。一方で、導出した運動方程式には\( \boldsymbol { r }’ \)が消え、本導出の解説以外の本記事に於いては、この\( \boldsymbol { r }’ \)を使用することがない。このことから、本導出の解説以外では、地軸から垂直に質点に向かうベクトルを改めて\( \boldsymbol { r }’ \)と定義し、遠心力の計算式は\( m ω ^ 2 \boldsymbol { r }’ \)となっている。従って、本導出の解説内の\( \boldsymbol { r }’ \)と本導出の解説以外の\( \boldsymbol { r }’ \)は別物なので注意されたし。 -
1項目
-
\( 2m \boldsymbol{ v }’ \times \boldsymbol{ ω } = \boldsymbol{ F_{corr} }’ \)
 コリオリ力
コリオリ力
-
\( mω^2 \boldsymbol{ r }’ = \boldsymbol{ F_{cen} }’ \)
 遠心力
遠心力
- コリオリ力(\( 2m \boldsymbol{ v }’ \times \boldsymbol{ ω } \))
-
- 大きさは、次のものに比例する。
- 物体の質量\( m \)
- 物体の速度ベクトル\( \boldsymbol{ v }’ \)の向きが一定であれば、速度ベクトルの大きさ
- 回転座標系の角速度ベクトル\( \boldsymbol{ ω } \)の向きが一定であれば、角速度ベクトルの大きさ(なお、本記事での回転座標系は地球なので、角速度ベクトルの向きも大きさも変化しない。)
- 向きは、ベクトル積(\( \boldsymbol{ v }’ \times \boldsymbol{ ω } \))の向きとなる。
- 地球の角速度ベクトル\( \boldsymbol{ ω } \)の大きさは非常に小さいので、コリオリ力は非常に弱い力である。
- 計算式に速度ベクトル\( \boldsymbol{ v }’ \)が存在すると言うことは、コリオリ力は非慣性系の地球上で運動している物体に対して発生することが分かる。逆に、地球上で静止している物体は、「 \( \boldsymbol{ v }’ = \boldsymbol{ 0 } \)」なので、コリオリ力が発生しないことになる。なお、大気も地球と一緒に自転しているので、大気内で運動する台風に対してコリオリ力が発生することになる。
- 大きさは、次のものに比例する。
- 遠心力(\( mω^2 \boldsymbol{ r }’ \))
-
- 大きさは、次のものに比例する。
- 物体の質量\( m \)
- 地軸から物体までの距離\( r’ \)(赤道に近い程、距離は長くなるので遠心力は強くなる。)
- 角速度ベクトル\( \boldsymbol{ ω } \)の大きさの2乗
- コリオリ力と違い、非慣性系(地球上)で静止している物体でも常に発生
- 向きは、地軸から遠ざかる方向(\( \boldsymbol{ r }’ \)の向き)
- 非常に小さい角速度ベクトル\( \boldsymbol{ ω } \)の大きさの2乗に比例するので、非常に弱い力である。
- 両極は地軸から物体までの距離\( r’ \)が0なので、遠心力が発生しない。
- 大きさは、次のものに比例する。
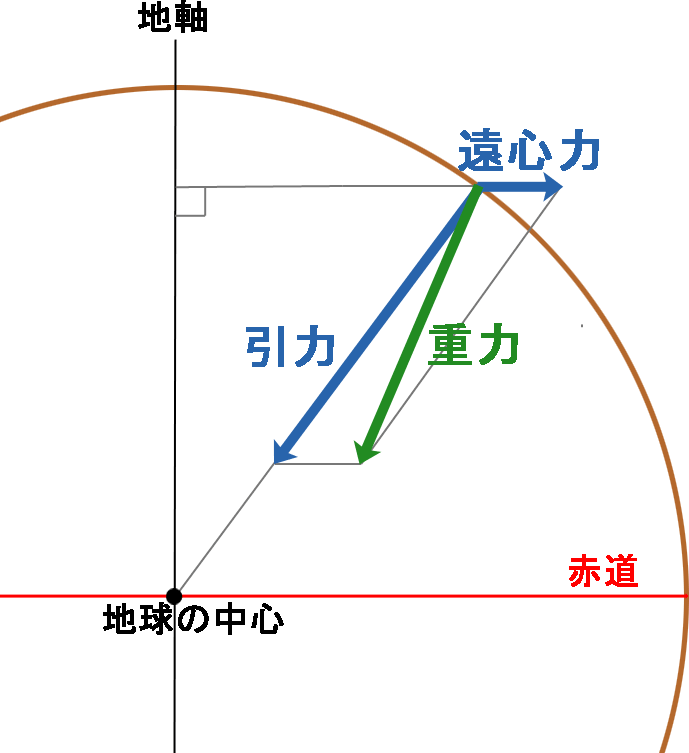
参考までに、重力とは、地球の中心に向かう万有引力と、地軸から垂直に遠ざかろとする遠心力の合力である。従って、両極と赤道以外の重力は、地球の中心に向かない(図5参照)。また、地球の半径は、極と赤道では異なり、赤道は極より21km長い。その理由は、遠心力が地球を膨らませているからである。遠心力は両極では発生しなく赤道に近づくほど強くなるので、赤道が最も膨らむことになり赤道半径が長くなる。
赤道のコリオリ力
本題に入る前に、コリオリ力の計算式にはベクトル積が存在することから、赤道のコリオリ力を考える上でベクトル積の理解は必須なので、まずはベクトル積の定義を述べておく。
- 向き
- 向きは、\( \boldsymbol{ a } \)と\( \boldsymbol{ b } \)に垂直であり、かつ\( \boldsymbol{ a } \)と\( \boldsymbol{ b } \)の始点を重ねた状態で、\( \boldsymbol{ a } \)を180度より小さい角度で\( \boldsymbol{ b } \)に重ねるために、始点を回転の中心として回転させる方向へ右ネジを回した時の、右ネジが進む方向である。
- 大きさ
-
大きさ\( | \boldsymbol{ a } \times \boldsymbol{ b } | \)は、\( | \boldsymbol{ a } | | \boldsymbol{ b } | \sin θ \)
(\( θ \):\( \boldsymbol{ a } \)と\( \boldsymbol{ b } \)の成す角度)であり、\( \boldsymbol{ a } \)と\( \boldsymbol{ b } \)を2辺とする平行四辺形OADB(図6の黄色)の面積に等しい。

まず、物体が東西南北の4方位に運動した時のコリオリ力を考えることにする。本記事では、赤道のコリオリ力について考察するので、北緯0度だけを考えれば良い。しかし、多少回りくどい解説になるかもしれないが、折角考察するのだから赤道のような極端な緯度だけを理解するのでなく、汎用性を持たせるために北緯の中緯度当たりを調べ、緯度との関係を明らかにした上で赤道に当てはめて考えることにする。その上で、赤道に関しては、4方位だけでなく、水平方向の全方位の運動に対し、コリオリ力がどのように変移するかを考察する。
4方位に於ける中緯度とコリオリ力の関係
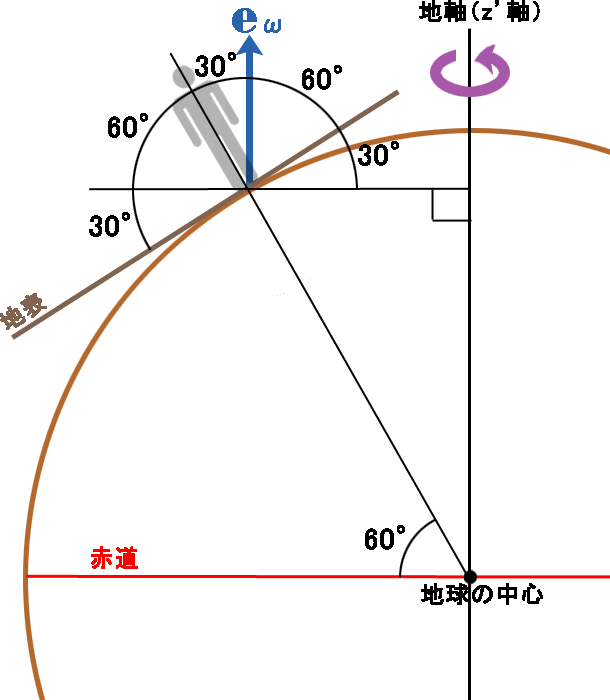
- 真東への運動
-
真西から真東へ速度\( \boldsymbol{ v }’ \)で水平方向に運動した場合である。
- 向き
-
右ネジを\( \boldsymbol{ v }’ \)から\( \boldsymbol{ e_ω } \)へ回した時の進む方向なので、真南(進行方向の右)向きの仰角30°(90°- 北緯60°)であり、地軸から遠ざかる方向、つまり遠心力と同じ向きとなる。
なお、真東への運動では、北緯何度であろうとコリオリ力は遠心力と同じ向きに働く。 - 大きさ
-
\( \boldsymbol{ v }’ \)と\( \boldsymbol{ e_ω } \)の成す角度は90°である。従って、\(2mω \boldsymbol{ v }’ \times \boldsymbol{ e_ω } \)の大きさは、\( 2mω | \boldsymbol{ v }’ | | \boldsymbol{ e_ω }| \sin 90^\circ \)\( = 2mωv’ \)となる(図8の緑色ベクトル参照)。
なお、\( \sin 90^\circ \)と言うことは、全方位の中で、大きさが最大になる向きの運動をしていることになるが、この時の水平成分の大きさは、\( 2mωv’ \cos ( 90^\circ – 北緯60^\circ ) \)\( = 2mωv’ \sin (北緯60^\circ ) \)\( = 2mωv’ \times 0.866 \)となる(図8の紫色ベクトル参照)。
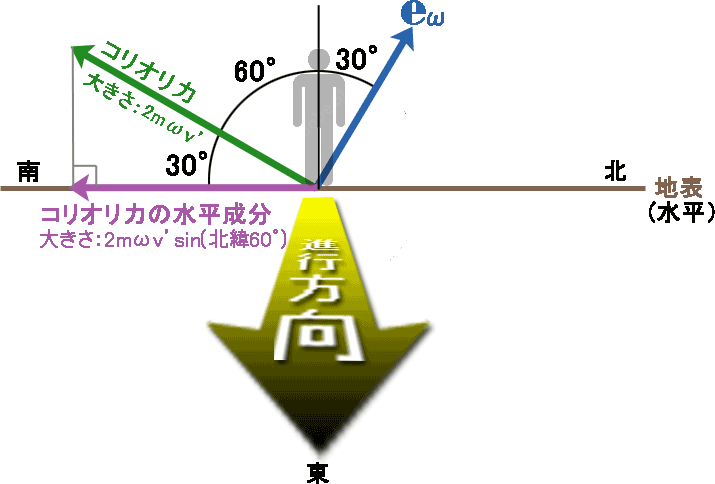 図8 進行方向の真東から見た図
図8 進行方向の真東から見た図 - 真西への運動
-
真東から真西へ速度\( \boldsymbol{ v }’ \)で水平方向に運動した場合である。
- 向き
-
右ネジを\( \boldsymbol{ v }’ \)から\( \boldsymbol{ e_ω } \)へ回した時の進む方向なので、真北(進行方向の右)向きの俯角30°(90°- 北緯60°)であり、地軸に近づく方向、つまり遠心力と逆向きとなる。
なお、真西への運動では、北緯何度であろうとコリオリ力は遠心力と逆向きに働く。 - 大きさ
-
\( \boldsymbol{ v }’ \)と\( \boldsymbol{ e_ω } \)の成す角度は90°である。従って、\(2mω \boldsymbol{ v }’ \times \boldsymbol{ e_ω } \)の大きさは、\( 2mω | \boldsymbol{ v }’ | | \boldsymbol{ e_ω }| \sin 90^\circ \)\( = 2mωv’ \)となる(図9の緑色ベクトル参照)。
なお、\( \sin 90^\circ \)と言うことは、全方位の中で、大きさが最大になる向きの運動をしていることになるが、この時の水平成分の大きさは、\( 2mωv’ \cos ( 90^\circ – 北緯60^\circ ) \)\( = 2mωv’ \sin (北緯60^\circ ) \)\( = 2mωv’ \times 0.866 \)となる(図9の紫色ベクトル参照)。
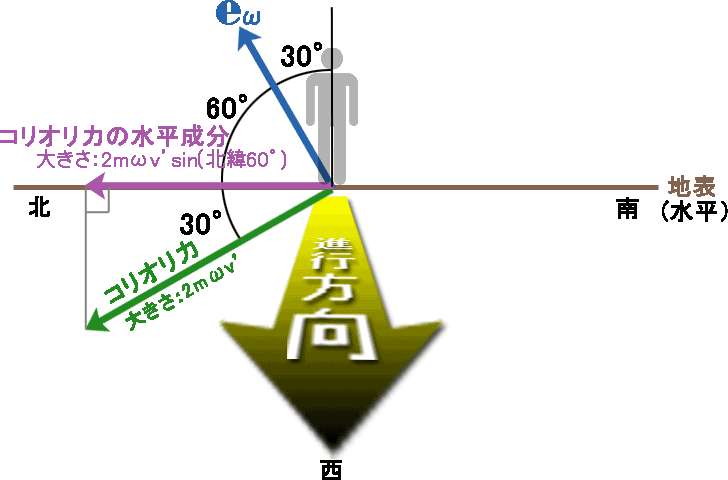 図9 進行方向の真西から見た図
図9 進行方向の真西から見た図 - 真北への運動
-
真南から真北へ速度\( \boldsymbol{ v }’ \)で水平方向に運動した場合である。
- 向き
-
右ネジを\( \boldsymbol{ v }’ \)から\( \boldsymbol{ e_ω } \)へ回した時の進む方向なので、真東(進行方向の右)向きとなり、仰角0°(地表に水平)となる。
なお、真北への運動では、北緯何度であろうとコリオリ力は地表と水平に働く。 - 大きさ
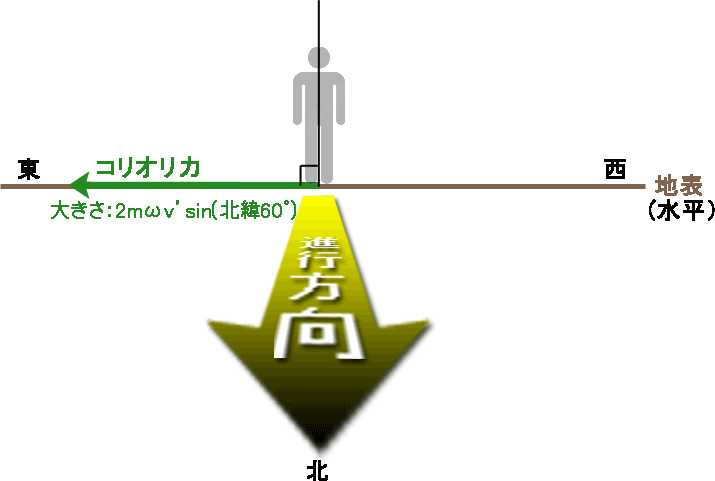 図10 進行方向の真北から見た図
図10 進行方向の真北から見た図 - 真南への運動
-
真北から真南へ速度\( \boldsymbol{ v }’ \)で水平方向に運動した場合である。
- 向き
-
右ネジを\( \boldsymbol{ v }’ \)から\( \boldsymbol{ e_ω } \)へ回した時の進む方向なので、真西(進行方向の右)向きとなり、仰角0°(地表に水平)となる。
なお、真南への運動では、北緯何度であろうとコリオリ力は地表と水平に働く。 - 大きさ
-
\( \boldsymbol{ v }’ \)と\( \boldsymbol{ e_ω } \)の成す角度は120°である(図11のオレンジ色枠参照)。従って、\(2mω \boldsymbol{ v }’ \times \boldsymbol{ e_ω } \)の大きさは、\( 2mω | \boldsymbol{ v }’ | | \boldsymbol{ e_ω }| \sin 120^\circ \)\( = 2mωv’ \times 0.866 \)となる(図11の緑色ベクトル参照)。
なお、この\( \sin 120^\circ \)を北緯を使って表すと\( \sin ( 180^\circ – 北緯60^\circ) \)であり、つまり\( \sin ( 北緯60^\circ) \)となる。
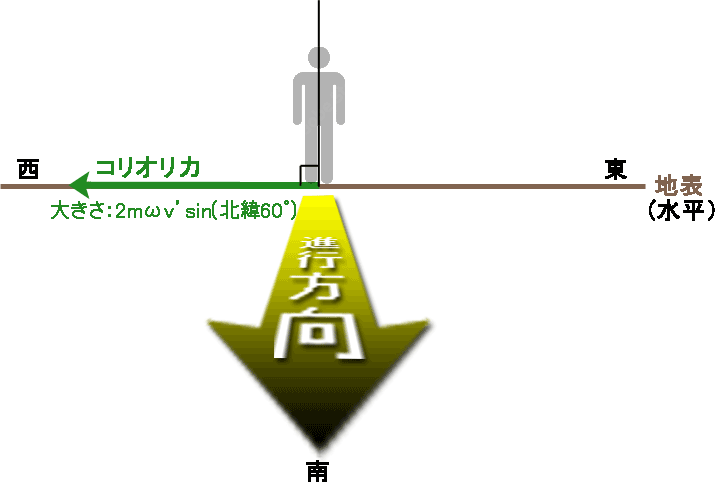 図11 進行方向の真南から見た図
図11 進行方向の真南から見た図
4方位に於ける北緯とコリオリ力の関係
- 真東への運動
-
- 向き
-
仰角「90°ー北緯」の真南(進行方向の右)向き。
※遠心力と同じ向き。 - 大きさ
-
\( 2mωv’ \)
※水平成分の大きさ:\( 2mωv’ \sin (北緯) \)
- 真西への運動
-
- 向き
-
俯角「90°ー北緯」の真北(進行方向の右)向き。
※遠心力と逆向き。 - 大きさ
-
\( 2mωv’ \)
※水平成分の大きさ:\( 2mωv’ \sin (北緯) \)
- 真北への運動
-
- 向き
-
水平の真東(進行方向の右)向き。
- 大きさ
-
\( 2mωv’ \sin (北緯) \)
- 真南への運動
-
- 向き
-
水平の真西(進行方向の右)向き。
- 大きさ
-
\( 2mωv’ \sin (北緯) \)
4方位に於けるコリオリ力の水平成分の大きさは、北緯何度のどの方位であろうと、常に\( 2mωv’ \sin (北緯) \)が成り立つことが分かる。
北緯0°(赤道)とコリオリ力の関係
4方位
- 真東への運動
-
- 向き
-
仰角「90°ー0°」の真南(進行方向の右)向き
 上向きの鉛直方向
上向きの鉛直方向
- 大きさ
-
\( 2mωv’ \) 〔水平成分:\( 2mωv’ \sin 0^\circ \)〕
 \( 2mωv’ \) 〔水平成分:0〕
\( 2mωv’ \) 〔水平成分:0〕
- 真西への運動
-
- 向き
-
仰角「90°ー0°」の真北(進行方向の右)向き
 下向きの鉛直方向
下向きの鉛直方向
- 大きさ
-
\( 2mωv’ \) 〔水平成分:\( 2mωv’ \sin 0^\circ \)〕
 \( 2mωv’ \) 〔水平成分:0〕
\( 2mωv’ \) 〔水平成分:0〕
- 真北への運動
-
- 向き
-
水平の真東(進行方向の右)向き
 下記の通り、大きさ0なので向き無し
下記の通り、大きさ0なので向き無し
- 大きさ
-
\( 2mωv’ \sin 0^\circ \)
 0
0
- 真南への運動
-
- 向き
-
水平の真西(進行方向の右)向き
 下記の通り、大きさ0なので向き無し
下記の通り、大きさ0なので向き無し
- 大きさ
-
\( 2mωv’ \sin 0^\circ \)
 0
0
全方位
なお、ここでは、方位を方位角で表すことにする。つまり、真北が0°(360°)となり、時計回りに、真東が90°、真南が180°、真西が270°となる。
- 向き
-
赤道に於ける地表の水平面は地軸と平行であることから、ベクトル積(\( \boldsymbol{ v }’ \times \boldsymbol{ e_ω } \))の向き、つまりコリオリ力の向きは、どの方位に運動しようと次の2つのどちらかになる。
- 方位角0°~180°(南北方向を境に切り分けた場合の東側)の運動
-
コリオリ力の向き
 上向きの鉛直方向(水平成分の大きさは0)
上向きの鉛直方向(水平成分の大きさは0)
- 方位角180°~360°(南北方向を境に切り分けた場合の西側)の運動
-
コリオリ力の向き
 下向きの鉛直方向(水平成分の大きさは0)
下向きの鉛直方向(水平成分の大きさは0)
- 大きさ
-
コリオリ力の大きさは\( 2mω | \boldsymbol{ v }’ \times \boldsymbol{ e_ω }| \)\( =2mω | \boldsymbol{ v }’ | | \boldsymbol{ e_ω }| \sin θ \)であり、赤道に於いては、θの値(\( \boldsymbol{ v }’ \)と\( \boldsymbol{ e_ω } \)の成す角度)が0°~180°の範囲で変移することから、\( \sin θ \)の値は0~1の範囲で変移する。従って、コリオリ力の大きさは、最小0~最大\( 2mωv’ \)の範囲で変移することになる。
\( \sin θ \)の値は、物体の運動の向きが方位角90°(真東)及び方位角270°(真西)で最大の1であり、方位角0°(真北)及び方位角180°(真南)に近づくにつれて減少して行き、方位角0°及び180°で0となる。従って、コリオリ力の大きさも同様で、物体の運動の向きが方位角90°(真東)及び方位角270°(真西)で最大の2mωv’であり、方位角0°(真北)及び方位角180°(真南)に近づくにつれて減少して行き、方位角0°及び180°で0となる。
結論

次の方どうぞ。

入らせてもらうで~。
和田アキ子と言いますわ。「アッコ」と呼んでええで~。
よろしゅう頼んます。

アッコさん。どうされました?

ウチな、台風が近づくだけで、片頭痛がすんねん。

あぁ、それね、台風頭痛と言って気象病の一種ですね。
内耳に気圧センサーがあり、極僅かな気圧の変化を察知し、それを脳がストレスと感じてしまうと、自律神経のバランスが乱れ、頭痛などに陥るんです。
敏感な方に起こる症状なので、心配いりませんよ。
はい、次の方。

あのな~、先生、まだ相談があんねん。

え~! まだあるの?

ウチが物を落とすと、地球の中心に落ちて行かんとって、少しずれて落ちていくように見えんねん。
その状況を見てまうと、めまいが起こり、体調不良に陥んねん。

それは、遠心力のせいだから、アッコさんだけに起きている訳じゃないのよ。
日本に住んでいる以上は諦めなさい。

海外に移住すれば何とかなりまっか?

そうね、遠心力が発生しない地域となると、近場では北極...
でも、今は冬真っ最中だから、ちょっと遠くなるけど南極はどう?

ウチ、冷え性やから、どっちも嫌でっせ。
どうせ移住するなら、ぬくいところがええねん。

わがままな方ね。
その男勝りの体格なら、体力に自身がありそうね?

自身ありまんがな。

そう言うことなら...
ケニア、コンゴ、ソマリアなどのアフリカとか、エクアドルやブラジルの南米など色々あるわよ。
アッコさんのようなわがままな方は、モルディブの水上コテージなんかどうかしら?

これらの国では、なんや、あの~「温泉力」ちゅうもんが働かないんでっか?

働くけど、遠心力の方向は引力と同じだから、重力の強さが変わるだけで、地球の中心からずれることがないのよ。

さよか...せやけど...
例え、ずれへんようになっても、結局「温泉力」のせいで重力の強さが変わってしまえば、自律神経が乱れ体調不良を引き起こせへんか心配やわ!

しょうがないわね。
「DoctorX」の名にかけて、ベストな治療方法を見つけてあげるから、ちょっと待ってなさい。

「失敗せぇへん先生」に、こないに親身になってもろて痛み入りますわ。

今から、高度な計算をするから静かにしてもらえるかしら?

御意!

患者は西側に走りさえすれば良い筈ね。
でも、名医である私は、患者の肉体的負担も考えて、最も負担の少ない真西を選択すべきだわ。
そんでもって、「遠心力=コリオリ力」の方程式は、「\( mω^2r’ = 2mv’ω \)」となるわね。
そこから、\( v’ \)を求めると...
\( v’ = ωr’ \div 2 \) となり、御茶の子さいさいよ。
ここで、\( ω \)と\( r’ \)の値は...
\( r’ \)は赤道半径の\( 6.378 \times 10^6 \)[m](6378km)になるわね。
角速度\( ω \)の大きさとなると...
地球は24時間で1周するから、
\( 2π \)[rad]\( \div (24 \times 60 \times 60) \)[s]\( \fallingdotseq 7.3 \times 10^{-5} \)[rad/s] と、スラスラ求まる私の才能が恐いわ。
後は、これらの値を\( v’ \)の式に代入し、こんな計算はちょちょいのちょいで、
\( v’ \fallingdotseq 233 \)[m/s]となり、「DoctorX」にかかれば屁の河童と。

ほ~ら治療方法が、もう見つかったわよ!
モルディブに移住したら、秒速233mで真西に突っ走れば良いだけよ。
アッコさん、さっき「体力には自信ある」と言ったわよね。楽勝でしょう。

それって、時速何キロでっか?

え~と、時速839キロよ。

......
そや、ウチには40年続いとる「アッコにおまかせ」があるんやった。
すぐに降板して海外に移住できまへんのや。
もう少し日本で我慢してみますわ。
健康が一番やさけ、先生も日頃から温泉にでも入って、「温泉力」に慣れるようにしとかなあかんで~。
ほな、さいなら。

は~い、次の方どうぞ~
日常会話に於いて、速さが遅くなれば「加速」でなく「減速」と表現し、一定速度で曲がっても「加速」と表現しなく、速さが速くなった時だけに「加速」と表現しているが、物理学では速度が変化する運動は全て「加速」と表現する。
なお、本題のコリオリ力も地球の自転により発生する見かけの力(慣性力)である(詳細は後述の「赤道ではコリオリ力が働かないの?」参照)。